Research
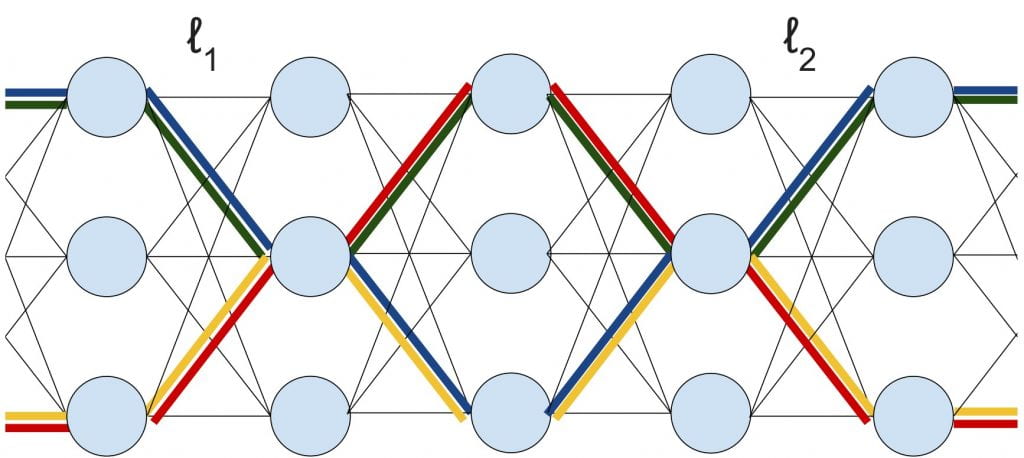
Finite Depth & Width Corrections to the Neural Tangent Kernel
(With Boris Hanan)
We prove the precise scaling, at finite depth and width, for the mean and variance of the neural tangent kernel (NTK) in a randomly initialized ReLU network. ICLR Spotlight.

Uniform Convergence to the Airy Line Ensemble
(With Duncan Dauvergne & Bálint Virág)
We prove a general theorem for uniform convergence to the Airy line ensemble that applies to many different last passage percolation settings
Solution of the Kolmogorov Equation for TASEP
(With Jeremy Quastel & Daniel Remenik)
We provide a direct and elementary proof that the transition probability formulas for TASEP solve the Kolmogorov backward equation. Published in Annals of Probability.
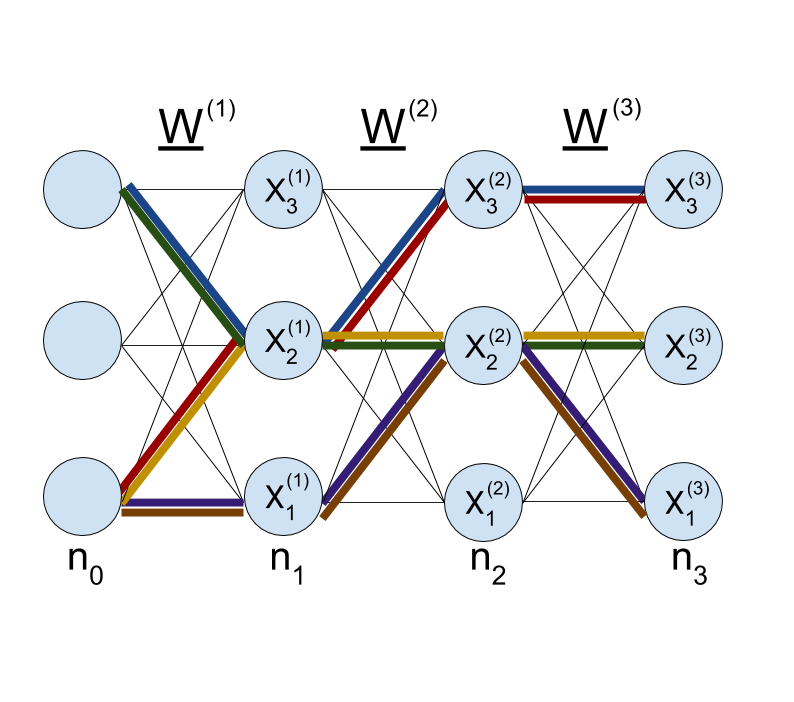
Products of Many Large Random Matrices and Gradients in Deep Neural Networks
(With Boris Hanin)
In this project, we prove a central-limit-type theorem for products of many random matrices. This result was motivated by deep neural nets, and provides a quantitative explanation for the vanishing and exploding gradient problem in deep neural networks. Slides available here. Published in Communications in Mathematical Physics.
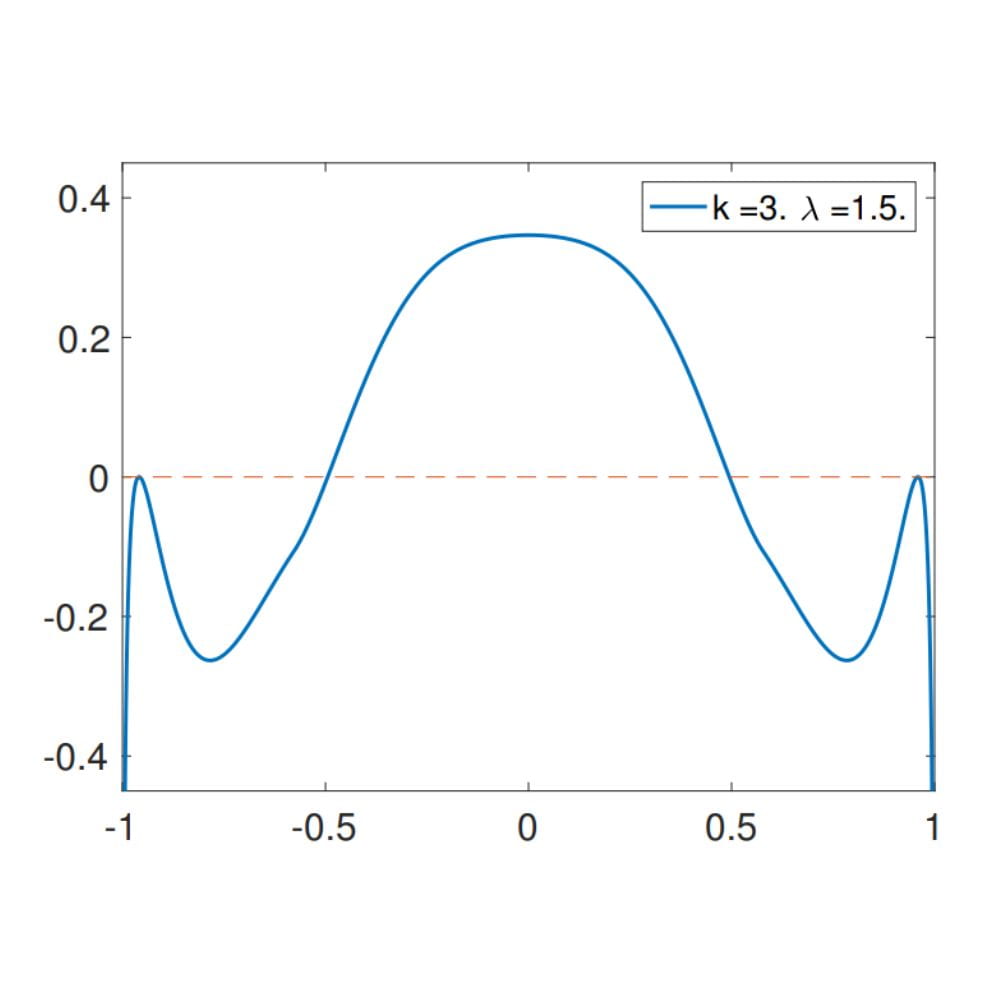
The Landscape of the Spiked Tensor Model
(With Gerard Ben Arous, Song Mei & Andrea Montanari)
In this project we study the energy landscape of a certain random function on the N dimensional hyper-sphere. This energy landscape is a natural model for certain problems in machine learning. We find a certain critical signal-to-noise ratio in this problem below which it becomes infeasible to detect the original signal. Slides available here. Published in Communications in Pure & Applied Math.
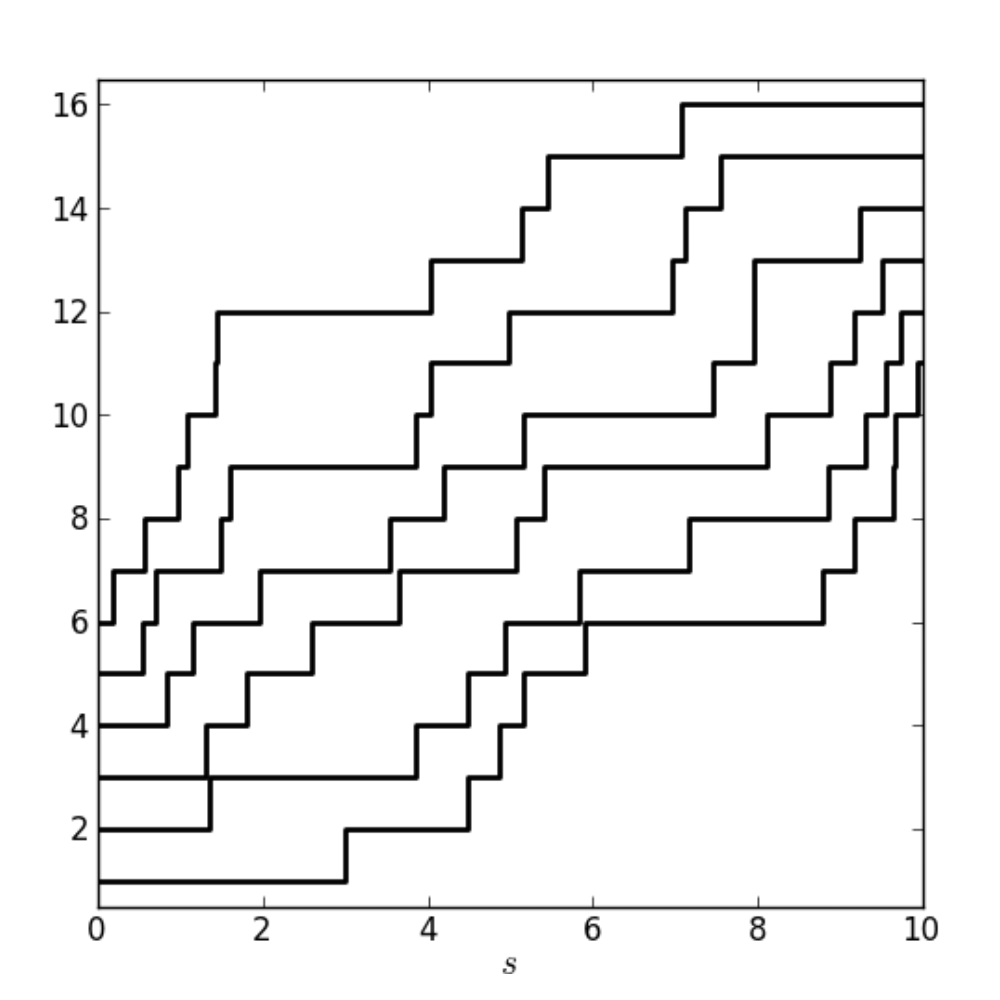
Intermediate Disorder Limits for Multi-layer Semi-Discrete Directed Polymers
I show convergence for semi-discrete directed polymers (also known as the O’Connell-Yor polymer) to the corresponding partition function for multi-layer continuum polymers. This convergence verifies, modulo a previously hidden constant, an outstanding conjecture proposed by Corwin and Hammond in their construction of the KPZ line ensemble.
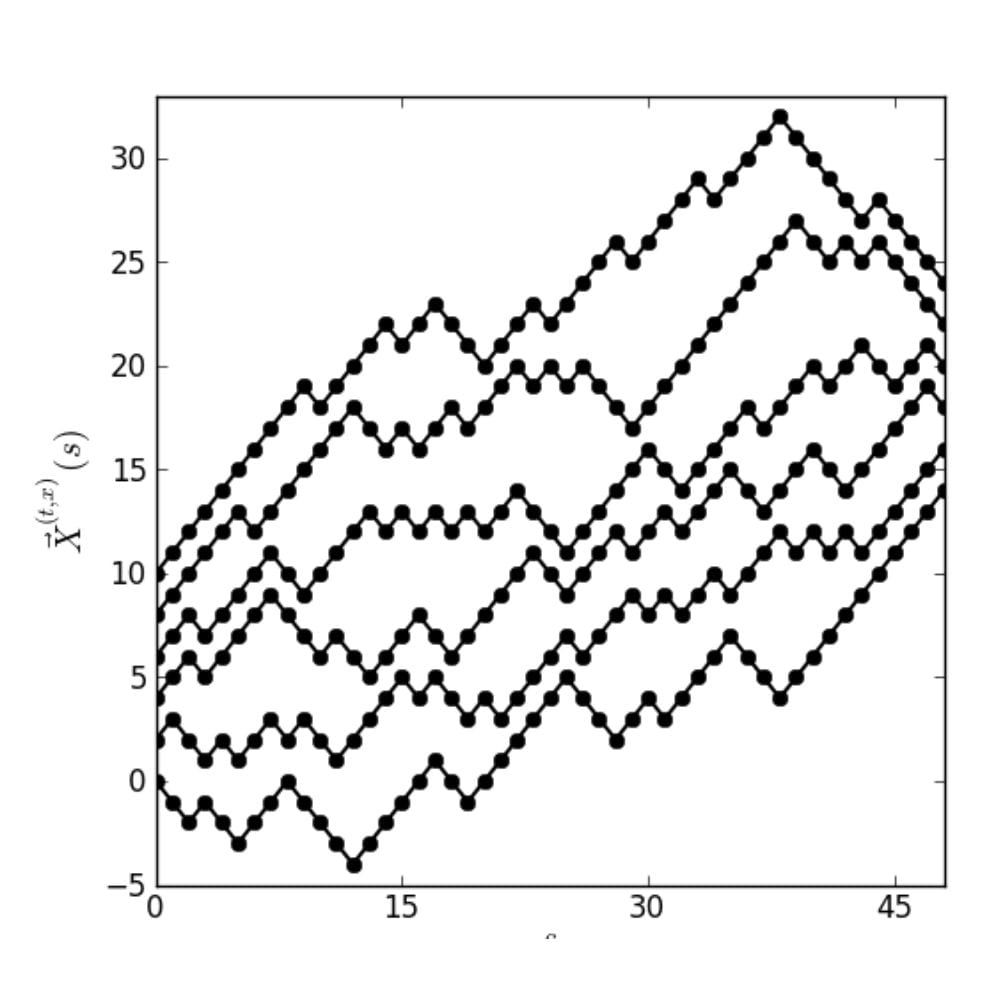
Intermediate Disorder Directed Polymers & the Multi-Layer Extension of teh Stochastic Heat Equation
(With Ivan Corwin)
A research project about the scaling limits of multiple non-intersecting directed polymers. We study the partition function of several non-intersecting walks in a random environment in the limit where the 1) the length of the walks goes to infinity 2) the randomness in the disorder goes to zero. If the rate of these two limits is tuned correctly, there is a non-trivial limit. The limit turns out to be related to the “multi-layer extension” of the stochastic heat equation. This whole construction can also be thought of as a limit for the geometric RSK process. Published in Electronic Journal of Probability.
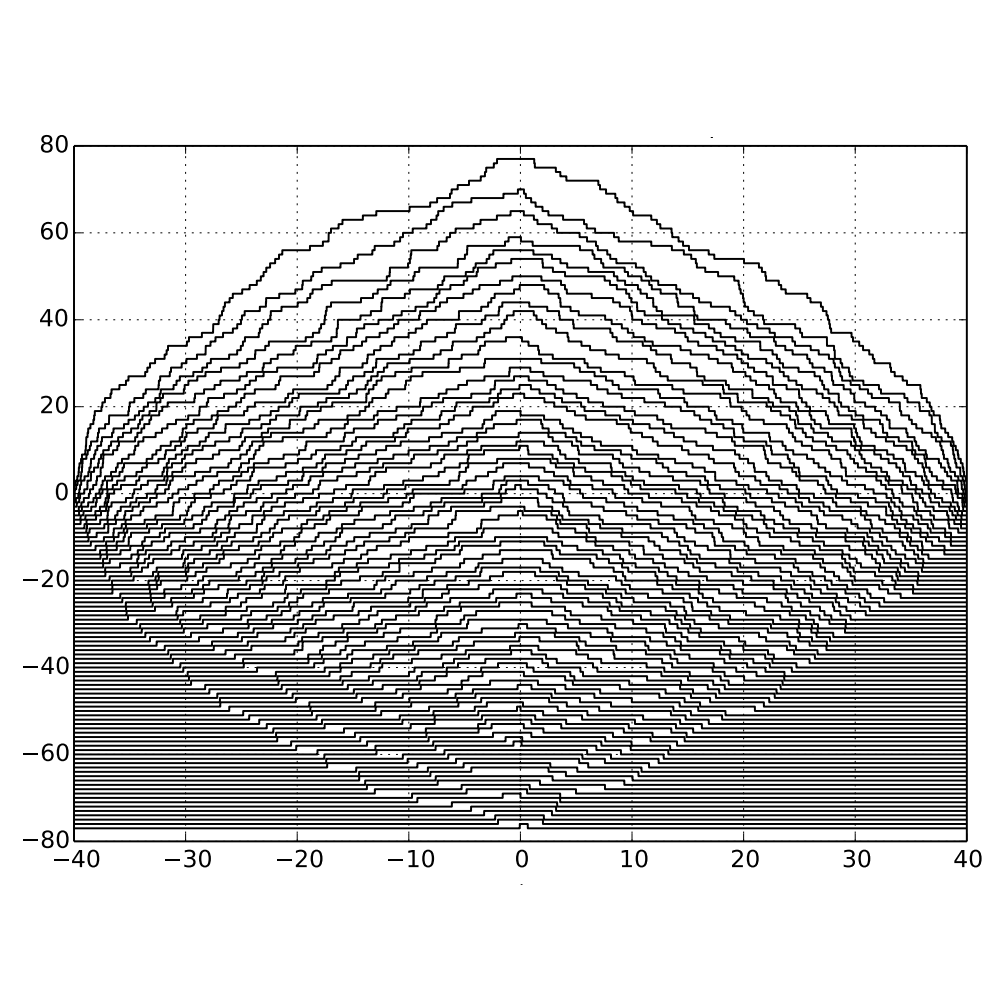
Decorated Young Tableaux and the Poissonized Robinson-Schensted Process
In this project, I generalized the definition of a Young Tableau to include real entries. By applying a generalization of the RS algorithm to a Poisson point process, we get a pair of random such generalized Tableau whose law is related to Schur processes and non-crossing Poisson walks. Published in Stochastic Processes and their Applications.
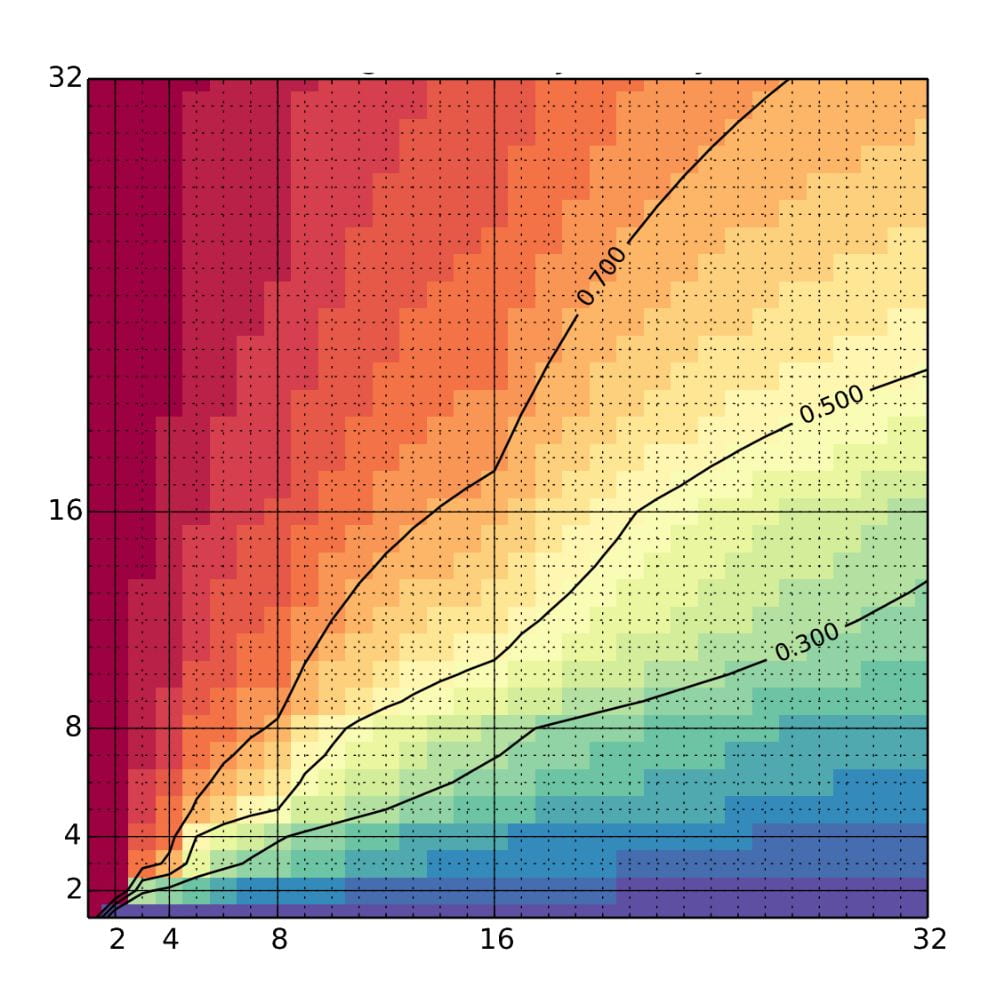
Optimal Strategy in “Guess Who?”: Beyond Binary Search
“Guess Who?” is a popular two player game where players ask “Yes” or “No” questions to search for their opponent’s secret identity from a pool of possible candidates. Common wisdom is that using a binary search approach to narrow down candidates is the best strategy. In this work, I showed that this is NOT the case for the player who is behind. Instead, the player who is behind should make certain bold plays to maximize their chance to win. I was able to find an exact formula for these bold plays and prove their optimality. Published in Probability in the Engineering and Informational Sciences.

Stabilization Time for a Type of Evolution on Binary Strings
(With Mike Noyes & Jacob Funk)
In this project, we considered a type of non-random TASEP-like evolution for particles on a finite line where particles deterministically move to the left under a simultaneous update rule. (This was presented in terms of binary strings in the paper). We found the limit law for the “stabilization time” for this update rule if you start with a random initial configuration. The limit law is Gaussian unless you start with a near-equal number of holes and particles…in which case an entirely different limit law is found. Published in the Journal of Theoretical Probability.
